Тайната на перфектното парти е скрита в задачата на Франк Рамзи

Вече 95 години учени се опитват да намерят решение, но дори компютрите не могат да се справят

Математика и парти се приемат като две взаимноизключващи се понятия. Математици и перфектното парти още повече.

Само добрите математици обаче могат да организират перфектното парти. Или поне само те могат да се справят със задачата на Рамзи, която дава отговора при колко гости ще имаме идеалното съотношение между приятели и непознати. Макар че понякога отговорът на тази задача е “никой не знае”.

Франк Рамзи е един от позабравените гении на математиката от 20-те години на миналия век. Още повече че той никога не е направил нещо особено, за да популяризира теориите си.

“Светът никога няма да проумее какво се случи, какво светило угасна”, пише на 9 януари 1930 г. белетристът Литън Страчи, виден член на лондонската литературна група Блумсбъри. В този ден, само на 26 години, умира преподавателят по математика в Кеймбридж Франк Рамзи, когото Страчи сравнява с Нютон.

Като научно наследство Рамзи оставя разработките си по спестовните ставки, които и до ден днешен са в основата на банковата система, каквато я познаваме.

Но приносът му в чистата математика е сбутан в друг текст, публикуван само веднъж преди 95 години и съдържащ две теореми. С тях математикът проучва методите за определяне на валидността на логическите формули. Повече от 40 години след публикуването им те се превръщат в основата на клона от математиката, известен като теорията на Рамзи, който

анализира реда и безредието

Именно на база на теоремите на Рамзи в наши дни оксфордският математик Мартин Гулд обяви, че сред всеки шестима потребители на фейсбук винаги ще има или трима взаимни приятели, или трима, между които няма никакви приятелски връзки.

Фундаменталният въпрос, който Рамзи си задава, е дали може да бъде намерен ред в хаоса. И колко голямо парче от хаоса е нужно, за да можем да го подредим.

Най-популярният пример за задача на Рамзи е именно с организирането на парти. Нека предположим, че в една стая се намират шестима случайно подбрани души. И ни интересува дали те се познават, или не. За решаване на задачата може да се ползва графика, на която с цвят да отбележим тези, които се познават един друг, и с друг цвят - непознатите. Ако се питате защо тази информация ни е нужна, за да организираме парти, то замислете се, ако трябва да разположите тези хора около една маса. Но така, че всеки да има хем сигурен събеседник, хем някой нов, с когото да му е интересно. За целта помагат триъгълниците от един цвят (познати или непознати), които можем да начертаем между шестимата души. А след това да разместим местата на масата.

Ако не вярвате, при шестима души винаги ще се намерят трима, които се познават или трима напълно непознати. Лошото е, че търсенето на комбинациите с прокарване на чертички е леко досадно.

При шестима имаме над 30 000 възможни комбинации,

които да проверим по бабешкия начин.

Ето тук на помощ идва Рамзи. Защото неговата задача дава отговор на въпроса “Колко души ни трябват, за да намерим трима познати или трима непознати?”. Тоест той отговаря на въпроса колко гости да поканим, за да ни се получи партито.

При горния пример с шестима души сметките са лесни. Числото на Рамзи се изписва като R (a,b). Тоест, ако искаме да сметнем формулата с трима познати и трима непознати, търсим R (3,3). Както видяхме вече, тук отговорът е шест.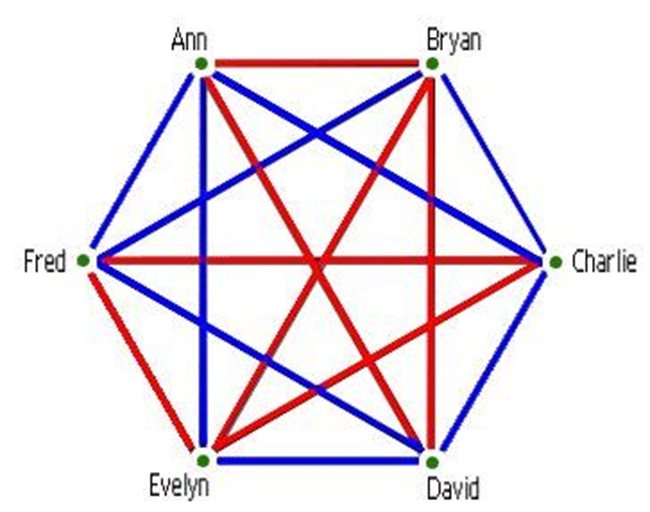

Естествено, в живота не правим партита само с шестима. И съответно ни е нужно да можем да сметнем и други числа.

Проблемът е, че тук става малко сложно. Примерно да намерим R (4,4), което е 18, обикновено трябва да сметнем първо R (3,4), което пък е 9. Като отново при тези комбинации може да ползваме графично решение с отсечки между отделните хора, които ще каним на гости. При по-големи числа обаче става малко сложно. Което превръща задачите на Рамзи в една от огромните математически загадки. Още повече че за повечето сметки не би могъл да ни помогне и компютър.

Всъщност много малко числа на Рамзи R(a, b) са известни (като a и b са по-големи от 2). Вече видяхме, че R (3,3)=6, R (4,3)=9 и R (4,4)=18. Освен това са известни само още три стойности: R (5,3)=14, R (6,3)=18 и R (7,3)=23. Но примерно за R (5,5) знаем само, че е някъде между 42 и 54.

При горната граница на R (5,5)=54 решението чрез графика ще ни коства прокарването на 1431 линии. А като вземем предвид, че всяка от тях може да е както между познати, така и между непознати реално трябва да прокараме невероятно количество линии - 10 на степен 400. За сравнение броят на частиците в познатата ни Вселена е само 10 на степен 80. Така че няма никакъв шанс дори и най-бързият възможен компютър да завърши такова търсене. Това е загадка, чийто отговор може би никога няма да узнаем.

Дотук има няколко значими пробива в решаването на тази нерешима задача. През 1935 г. Пол Ердьош установява, че всяко число на Рамзи е 4 на степента на размера на кликата. След което уточнява, че намирането на точното число на Рамзи за клика от шест души е толкова трудно, че ако извънземните поискат да се опитаме да го изчислим или да бъдем унищожени, няма да имаме друг избор, освен да се опитаме да ги атакуваме първи.

Наскоро обаче Джулиън Сахасрабуде от Кеймбридж показа, че горната граница за числата на Рамзи може да бъде намалена от 4 на степента на размера на кликата до 3.993 на степента на размера на кликата.

За този “прогрес” екипът на Сахасрабуде работи от 2018 г. Като някъде в средата на работата си решават, че трябва да пренапишат доказателството си. Което и в момента е разписано върху повече от 50 страници и предстои да бъде проверено. Но пък разпали желание сред математиците да намерят още по-ниска горна граница на Рамзи. И евентуално някой ден да открият тайната на перфектното парти.